A curious guide to Entropy: Part 1 - Thermodynamics & Maxwell’s Daemon
I still remember it like it was yesterday. I started working with decision trees about 10 years ago. And they were exciting. Calculating information gain, determining the best splits and features.
But with all the excitement, I still had the sinking feeling: So what?
You probably know this feeling. You go through the motions, you solve a complex problem, but yet “there is more to understand”. It’s like eating a fast food pizza when your body is really craving a salad.
I believe everything is better understood in context. And that’s why you are reading this article today.
This is the first one in a three-part series that looks at the idea of measuring disorder, also known as entropy, from its roots in thermodynamics to how we know (and love it) today in decision tree algorithms. This is a beginner-friendly introduction. Thou shall not be afraid.
James Clerk Maxwell was a Scottish physicist. And if he had had a social media account he would have been swept with a flood of responses after his book “Theory of Heat” was released in 1871. In his book, he introduced a paradox which became known as “Maxwell’s Daemon” and stirred up the scientific community of the time.
Heated debaters saw the implications as far-reaching as refuting the 2nd Law of Thermodynamics.
But, wait, you might ask: What is the 2nd Law of Thermodynamics?
Let’s take a small step back.
Thermodynamics is the study of heat and thermal energy. You can think of it as the theoretical underpinning of steam engines that were developed in the 19th century.
To not make this too boring, let’s look at a simple example. You.
Your body can be formally seen as a system. You put energy into the system, e.g. by eating food (or reading this excellent article). In turn, the energy you put into the system gets transformed.
Energy is a system’s potential to “get stuff done” (do work).
Maybe you had your breakfast – two tasty hard-boiled eggs and a sandwich. Your breakfast is chemical energy. When you hit the road later with your running shoes you transform that chemical energy into kinetic energy (also called mechanical energy): you are moving your body and muscles.
An analogy would be to think of it as being similar to water. Water comes in different forms. Water being “water” (liquid water) or ice (frozen water), or steam (very hot water). The water is always there, it just changes its form. And that’s exactly what happens with energy. It changes form.
Okay, so you are still running. You are 10 minutes into your run, your muscles warm up and you are skilfully navigating around the pedestrians in front of you. As time goes on, your breathing gets heavier, your heart beats faster and you start sweating. (YESS!)
In thermodynamics terms, you are now starting to experience “heat loss”. Heat loss is unfortunate. We just learned about you being a beautiful isolated system in which energy gets transformed from one form to another. But it’s not all rosy. With heat loss, the initial energy is “still there”, it gets transformed but into a form that can’t be used anymore. This heat loss is also called entropy.
Entropy is a form of energy that can’t be used anymore to do work (“get stuff done”)
In an isolated system, like you when running, entropy will always increase until it reaches a maximum value. And this is the 2nd Law of Thermodynamics: “In an isolated system, entropy will always increase until it reaches a maximum value”.
2nd Law of Thermodynamics: In an isolated system, entropy will always increase until it reaches a maximum value.
What’s an implication of this? Well, if you keep running, your body will eventually not have enough (chemical) energy that can be transformed into kinetic one. So, if nothing is done entropy will reach a maximum and this is bad news for you. Entropy overload. So what do you do? You treat yourself to an amazing lunch.
BUT: And here comes the crucial thing to understand: This requires additional work. Entropy by itself (heat loss) will not decrease on its own. Additional work is required, you need to get that meal.
A core implication of the 2nd Law of Thermodynamics is that entropy in an isolated system can only be reduced by exerting additional work. It won’t reduce on its own.
Welcome back, amazing. You just learned the 2nd Law of Thermodynamics and how decreasing entropy requires additional work. You are now well prepared to follow the main act of today: Maxwell’s Daemon and his social media account.
One important info: Entropy is also referred to as a measure of order/disorder and this is how it will be used in the following.
High entropy = Large disorder. Low entropy = Little disorder.
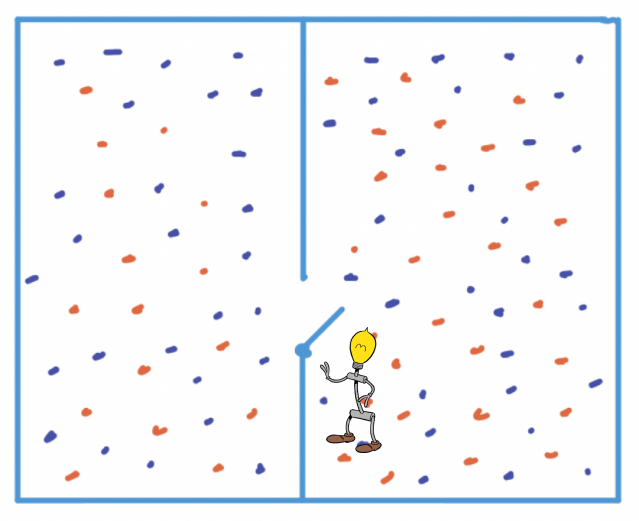
You might think the daemon in Maxwell’s thought experiment is evil but actually it’s not. It is simply a very small being guarding a door that connects two different rooms. For the fun of it, let’s assume it’s a club. And so the being can be thought of as a bouncer.
Figure 1: Maxwell's bouncer beginning her shift
When the daemon starts her shift, people (or air molecules) are all over the place. Entropy is high. The daemon is sad. But since there are club regulations, there is a general dance floor on the left and one for Very Important Particles on the right.
CLUB POLICY: This a low entropy club
So what the daemon does is that she opens and closes the door to let people pass through or deny them entry.
Over a long time, this leads to the following situation.
Figure 2: Maxwell’s bouncer at 4 am (happy)
All particles have been sorted into two groups: slower moving ones on the left, faster (very important) ones on the right. Entropy is low now. The bouncer is quite happy.
But now we come to the juicy part of the story: The argument Maxwell made is that it is possible to build the apparatus for opening and closing the door in a way that exerts minimal to no work.
HELLO? Didn’t we just learn that in an isolated system entropy can’t decrease by itself and tends by itself to a maximum?
OH, OH: The 2nd Law of Thermodynamics just got violated. Entropy can’t decrease without additional work. 🚨
And this is the fundamental reason why Maxwell’s “Theory of Heat” led to the explosion of his (theoretical) Twitter account.
Whether Maxwell was right or not continued to occupy scientists busy for decades. There were supporters of his ideas but also some who felt that Maxwell was sweeping something important under the rug.
The one who figured out what it was that Maxwell swept under the rug was Leo Szilard, a Hungarian mathematician. He is a key actor in part 2 of this series.
This article was a first introduction to the idea of Entropy. If you are interested in more of my writing and related ideas to this topic please subscribe to my newsletter.